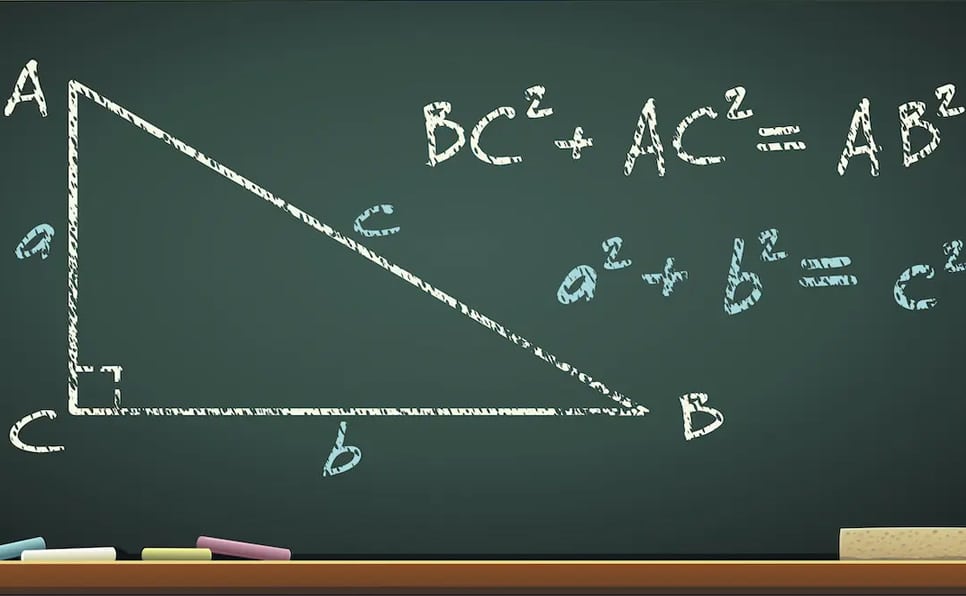En géométrie, les triangles occupent une place importante, notamment le triangle rectangle. Dans cet article, nous découvrirons comment savoir si un triangle est rectangle, en utilisant diverses méthodes dont le célèbre théorème de Pythagore et d’autres techniques qui vous faciliteront la tâche lorsqu’il s’agit de manipuler ces figures géométriques.
Le théorème de Pythagore
Le théorème de Pythagore est sans doute l’une des méthodes les plus connues pour vérifier qu’un triangle est rectangle ou non. Ce théorème énonce que dans un triangle rectangle, le carré de la longueur de l’hypoténuse (le côté opposé à l’angle droit) est égal à la somme des carrés des longueurs des deux autres côtés. En termes mathématiques :
- a² + b² = c² (où a et b représentent les longueurs des deux côtés adjacents à l’angle droit et c représente la longueur de l’hypoténuse)
Pour vérifier si un triangle est rectangle en utilisant ce théorème, il suffit donc de calculer les longueurs des côtés du triangle et de vérifier si leur relation correspond à celle décrite par le théorème de Pythagore.
Exemple pratique
Imaginons que nous ayons un triangle ABC avec les longueurs de côtés suivantes : AB = 3, BC = 4 et AC = 5. Pour vérifier si ce triangle est rectangle :
- Calculons le carré des longueurs pour chaque côté : AB² = 9, BC² = 16 et AC² = 25
- Vérifions l’égalité suivante : AB² + BC² = AC², c’est-à-dire 9 + 16 = 25 (25 = 25)
Puisque cette égalité est vraie, nous pouvons conclure que le triangle ABC est rectangle.
Le critère de perpendicularité
Outre le théorème de Pythagore, il existe une autre méthode pour déterminer si un triangle est rectangle : le critère de perpendicularité. Ce critère se base sur le produit scalaire de deux vecteurs . En effet, deux vecteurs sont perpendiculaires si et seulement si leur produit scalaire est nul.
Mise en application du critère
Pour appliquer ce critère à un triangle, il suffit d’effectuer les calculs suivants :
- Déterminer les coordonnées de trois points A, B et C qui forment le triangle
- Construire deux vecteurs à partir des points choisis, par exemple &overrightarrow;AB et &overrightarrow;BC
- Calculer le produit scalaire de ces deux vecteurs, et vérifier s’il est égal à zéro
Si le produit scalaire est égal à zéro, alors l’angle formé par les deux côtés du triangle est droit, et par conséquent, le triangle est rectangle.
La réciproque du théorème de Pythagore
Il existe également une autre méthode pour vérifier si un triangle est rectangle : la réciproque du théorème de Pythagore. Cette méthode consiste à inverser l’énoncé du théorème de Pythagore. Elle stipule que si dans un triangle, le carré de la longueur d’un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle.
Application de la réciproque
Prenons un exemple : supposons qu’on ait un triangle DEF avec les longueurs de côtés suivantes : DE = 5, EF = 12 et DF = 13. Pour savoir si ce triangle est rectangle :
- Calculons le carré des longueurs pour chaque côté : DE² = 25, EF² = 144 et DF² = 169
- Vérifions que l’une des relations suivantes est vraie :
- DE² + EF² = DF², soit 25 + 144 = 169 (169 = 169)
- DE² + DF² = EF², soit 25 + 169 = 144 (194 ≠ 144)
Comme la première relation est vraie, nous pouvons affirmer que le triangle DEF est rectangle.
Synthèse des méthodes
Nous avons présenté plusieurs approches pour déterminer si un triangle est rectangle :
- Le théorème de Pythagore et sa réciproque, qui se basent sur les longueurs des côtés du triangle
- Le critère de perpendicularité utilisant les produits scalaires des vecteurs formés par les côtés adjacents
Ces méthodes sont complémentaires et offrent une base solide pour résoudre divers problèmes impliquant des triangles rectangles. N’hésitez pas à les mettre en pratique lors de vos exercices de géométrie ou dans d’autres domaines nécessitant la manipulation de figures géométriques.